
Q) The length and breadth of a rectangle are in the ratio 3 : 2 and their perimeter is 2000 metres. If the length is increased in the ratio 1 : 2 and the breadth is increased in the ratio 2 : 3, then find out the proportion of resulting rectangle area to the existing rectangle area.
7 : 8
4 : 5
5 : 2
3 : 1
9 : 8
Solution: Let us take the length of the rectangle as '3x' and breadth as '2x'.
Perimeter of the rectangle is 2 x (length + breadth) = 2000 metres i.e. 2 x (3x + 2x) = 2000
2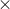 (5x) = 2000
(5x) = 2000
10x = 2000
x = 2000/10 = 200
Therefore, the length = 3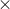 200 = 600 metres
200 = 600 metres
Breadth = 2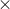 200 = 400 metres
200 = 400 metres
Area of the existing rectangle = Length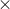 Breadth
Breadth
= 600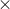 400
400
= 240000 sq. mts
If the length is increased in the ratio 1 : 2, then new length = 600/1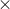 2 = 1200 metres
2 = 1200 metres
If the breadth is increased in the ratio 2 : 3, then new breadth = 400/2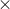 3 = 600 metres
3 = 600 metres
Area of resulting rectangle = 1200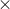 600 = 720000 sq. mts
600 = 720000 sq. mts
Therefore, the proportion of resulting rectangle area to the existing rectangle area is 720000 : 240000
i.e. 3 : 1
Solution: Let us take the length of the rectangle as '3x' and breadth as '2x'.
Perimeter of the rectangle is 2 x (length + breadth) = 2000 metres i.e. 2 x (3x + 2x) = 2000
2
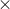 (5x) = 2000
(5x) = 200010x = 2000
x = 2000/10 = 200
Therefore, the length = 3
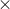 200 = 600 metres
200 = 600 metresBreadth = 2
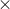 200 = 400 metres
200 = 400 metresArea of the existing rectangle = Length
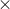 Breadth
Breadth= 600
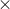 400
400= 240000 sq. mts
If the length is increased in the ratio 1 : 2, then new length = 600/1
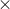 2 = 1200 metres
2 = 1200 metresIf the breadth is increased in the ratio 2 : 3, then new breadth = 400/2
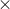 3 = 600 metres
3 = 600 metresArea of resulting rectangle = 1200
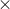 600 = 720000 sq. mts
600 = 720000 sq. mtsTherefore, the proportion of resulting rectangle area to the existing rectangle area is 720000 : 240000
i.e. 3 : 1


Post a Comment